Selamat datang di perpustakaan online di kelas bu Tutik! Mari kita saling mengenal sebelum memulai pembelajaran. Saya akan menjadi teman belajar kalian selama setahun dan berharap kita bisa berkolaborasi serta menikmati perjalanan belajar ini bersama!
Hari/tanggal : Selasa, 26 Agustus 2025
Kelas : VI AL JAZARI
Materi Muatan Pelajaran
B. Indonesia : Bab 2: Musisi Indonesia di Pentas Dunia
Matematika : Pecahan
CP Bahasa Indonesia
Bahasa Indonesia:
Capaian Pembelajaran:
Peserta didik mampu menjelaskan kembali ide pokok dan beberapa ide pendukung dari teks informasional, berpartisipasi aktif dalam diskusi dengan mempresentasikan gagasan, dan mampu menulis laporan sederhana (hasil wawancara) untuk menyampaikan informasi.
Tujuan Pembelajaran:
Murid dapat :
1. Memahami isi artikel tentang musisi Indonesia dan diplomasi budaya serta menjawab pertanyaan pemahaman.
2. Membuat peta pikiran untuk mengorganisasi gagasan tentang potensi diplomasi lunak Indonesia.
3. Merancang dan melakukan wawancara sederhana untuk menggali informasi tentang seni budaya lokal.
4. Menuliskan hasil wawancara dalam bentuk laporan singkat yang informatifCP Matematika:
Pada akhir fase C, peserta didik dapat menunjukkan pemahaman dan intuisi bilangan (number sense) pada bilangan cacah sampai 1.000.000. Mereka dapat membaca, menulis, menentukan nilai tempat, membandingkan, mengurutkan, melakukan komposisi dan dekomposisi bilangan tersebut. Mereka juga dapat menyelesaikan masalah yang berkaitan dengan uang. Mereka dapat melakukan operasi penjumlahan, pengurangan, perkalian, dan pembagian bilangan cacah sampai 100.000. Mereka juga dapat menyelesaikan masalah yang berkaitan dengan KPK dan FPB. Peserta didik dapat membandingkan dan mengurutkan berbagai pecahan termasuk pecahan campuran, melakukan operasi penjumlahan dan pengurangan pecahan, serta melakukan operasi perkalian dan pembagian pecahan dengan bilangan asli. Mereka dapat mengubah pecahan menjadi desimal, serta membandingkan dan mengurutkan bilangan desimal (satu angka di belakang koma)
Tujuan Pembelajaran :
Murid dapat melakukan operasi hitung perkalian dan pembagian pecahan.
Apa kabar anak sholih sholihah
Semoga semuanya dalam keadaan sehat wal'aafiyat
Mari kita awali dengan membaca doa terlebih dahulu semoga kita selalu sehat dan diberikan kemudahan dalam melaksanakan kegiatan belajar hari ini!
BAHASA INDONESIA
Pada pembelajaran Bahasa Indonesia kelas VI Kurikulum Merdeka terdapat pembahasan tentang Memahami Bacaan “Seni sebagai Kekuatan Diplomasi Budaya”. Tujuan pembelajaran kali ini adalah peserta didik dapat memahami ide pokok dan ide pendukung dari suatu artikel.
Paragraf adalah kumpulan dari sejumlah kalimat dari suatu teks bacaan. Biasanya ditandai dengan adanya bagian yang menjorok ke dalam atau ke kanan, pada setiap awal paragraf.
Setiap paragraf memiliki gagasan pokok dan gagasan pendukung. Gagasan pokok adalah ide utama atau inti utama yang dibahas dalam suatu paragraf. Gagasan pokok disebut juga sebagai ide pokok, gagasan utama, ide utama, atau pokok pikiran. Sementara itu, gagasan pendukung adalah informasi tambahan untuk mendukung gagasan pokok. Gagasan pendukung ini dapat ditemukan pada kalimat penjelas.

Berikut ini langkah-langkah cara menemukan ide pokok dan ide pendukung dalam suatu bacaan
- Baca judul dan paragraf pendahuluan dengan cepat dan teliti. Berdasarkan judul dan paragraf pendahuluan tersebut, rumuskan ide pokok bacaan.
- Untuk membuktikan ketepatan dugaan gagasan pokok yang telah dibuat, baca secara cepat paragraf-paragraf berikutnya.
- Bacalah kalimat- kalimat utama saja. Jika terdapat subjudul, bacalah sub-subjudul tersebut, dan kaitkan dengan pokok pikiran yang telah diduga.
- Jika dugaan benar, maka dapat dikatakan telah bisa merumuskan secara tepat ide pokok bacaan tersebut.
Cara Menentukan Ide Pendukung
Ide pendukung berguna untuk memperjelas ide pokok. Berikut adalah cara menentukan ide pendukung dalam suatu bacaan.
- Setelah memahami ide pokok, lanjutkan membaca paragraf-paragraf yang ada dalam tubuh bacaan secara cepat.
- Ketika membaca paragraf-paragraf tersebut, jangan lupa memerhatikan hubungan-hubungan antarkalimat, seperti: sebab-akibat, urutan waktu, hubungan tempat, hubungan masalah dan penyelesaiannya, atau hubungan orang-orang yang terlibat.
- Usahakan untuk tetap mengingat ide pokok setiap paragraf, dan memahami hubungan-hubungan antarkalimat yang ada.
Dengan mengetahui cara menemukan ide pokok dan ide pendukung, maka akan mempermudah dalam menyusun ringkasan. Ringkasan adalah bentuk singkat yang disarikan dari tulisan panjang tanpa mengurangi ide pokok.
Seni sebagai Kekuatan Diplomasi Budaya
Apa yang ada di pikiran kalian ketika mendengar kata Jepang? Kemungkinan besar kalian akan menyebutkan sushi, kimono, Doraemon, dan Naruto. Bagaimana dengan negara Australia? Mungkin kalian akan mengingat Opera House, koala, dan kanguru. Kalau Amerika Serikat disebut, yang ada di benak sebagian besar orang adalah film-film dari Disney atau produksi Hollywood, burger, dan ayam goreng.
Produk budaya yang dikenal oleh masyarakat dunia adalah modal suatu negara untuk melakukan diplomasi lunak (soft diplomacy). Diplomasi adalah suatu seni dan praktik untuk bernegosiasi yang dilakukan oleh negara atau organisasi. Diplomasi lunak menggunakan cara-cara yang halus untuk memengaruhi opini masyarakat akan suatu negara. Lawan dari diplomasi lunak adalah diplomasi keras, misalnya dengan menggunakan kekuatan militer.
Dan seterusnya.....
Kalian telah membaca artikel “Seni sebagai Kekuatan Diplomasi Budaya”di atas. Sekarang, diskusikan pertanyaan-pertanyaan berikut dengan teman-teman dalam kelompok!
1. Setujukah kalian bahwa budaya populer Korea digemari oleh banyak kalangan di Indonesia?
Budaya populer Korea seperti drama, fashion, makanan, dan K-pop banyak digemari di Indonesia.
2. Apa yang dimaksud dengan istilah ‘industri tanpa cerobong asap’?
Cerobong asap adalah simbol dari pabrik yang menggunakan mesin dan menghasilkan asap. Industri tanpa cerobong asap artinya industri yang tidak menggunakan pabrik untuk menghasilkan sesuatu, misalnya industri musik dan film yang karyanya dibuat tanpa pabrik.
3. Mampukah Indonesia mengikuti jejak Korea dalam menyebarkan budaya ke seluruh dunia?
Keberhasilan Indonesia menyebarkan budaya seperti gelombang Korea sangat dipengaruhi oleh kerja sama yang baik dari semua pihak, pemerintah yang mendukung dan pelaku industi kreatif yang bekerja keras menghasilkan karya terbaiknya.
4. Menurutmu, apa yang dapat dilakukan Indonesia untuk melakukan ‘diplomasi lunak’?
Indonesia mempunyai banyak potensi untuk melakukan diplomasi lunak melalui seni budaya, makanan, pariwisata, dan lain-lain. Keberhasilan gelombang Korea sangat dipengaruhi oleh kerja sama yang baik dari semua pihak, pemerintah yang mendukung dan pelaku industi kreatif yang bekerja keras menghasilkan karya terbaiknya.
Demikian pembahasan mengenai Memahami Bacaan “Seni sebagai Kekuatan Diplomasi Budaya”a. Semoga tulisan ini bermanfaat.
Sumber : Buku Bahasa Indonesia Kelas VI Kurikulum Merdeka, Kemendikbud.
MATEMATIKA
embahasan tentang Pecahan, Bilangan Desimal, dan Bilangan Bulat. Tujuan kegiatan pembelajaran kali ini adalah peserta didik mampu memikirkan cara untuk mengekspresikan hasil bagi pembagian bilangan bulat dalam pecahan dan untuk memahami konversi, memahami keterkaitan antara pecahan, desimal, dan bilangan bulat, dan mampu menyatakan pecahan sebagai desimal dan bilangan bulat, serta menyatakan desimal dan bilangan bulat sebagai pecahan, dapat melihat bahwa pecahan berada dalam kelompok angka yang sama dengan bilangan bulat dan desimal.
Pecahan, Bilangan Desimal, dan Bilangan Bulat
Pecahan adalah bagian dari satu keseluruhan dari suatu kuantitas tertentu. Secara matematis, bilangan pecahan dapat disimbolkan dengan “a/b”. Bilangan a/b bisa dibaca dengan “a per b”. Bilangan a sebagai pembilang dan bilangan b sebagai penyebut. Bilangan desimal adalah bilangan yang terdiri dari bilangan bulat dan bilangan pecahan, yang dalam penulisannya antara bilangan bulat dan pecahan dipisahkan dengan tanda koma, yang disebut dengan koma desimal. Bilangan bulat adalah semua bilangan yang tidak berbentuk pecahan atau desimal.
Pada kegiatan ini dengan mengelompokkan bilangan menjadi tiga kategori, peserta didik dapat menyadari fakta bahwa ada bilangan yang tidak dapat direpresentasikan dengan desimal.
1. Hasil Bagi dan Pecahan
Pikirkan tentang cara mengekspresikan hasil perhitungan selain bilangan bulat dan desimal.
1. Ketika kita membagi secara rata 2 l susu diantara ... anak, berapa l yang akan diterima setiap anak?
2 : ...
1. Masukkan bilangan dari 1 sampai 5 di dalam kotak dan hitunglah hasilnya.
2. Bagilah pernyataan di atas menjadi 3 kelompok berdasarkan jawabannya.
A. Yang jawabannya bilangan bulat.
2 : 1, dan 2 : 2
B. Yang jawabannya dinyatakan dengan tepat sebagai bilangan desimal.
2 : 4 dan 2 : 5
C. Yang jawabannya tidak dinyatakan dengan tepat sebagai bilangan desimal.
2 : 3 adalah 0,666..., jadi bilangan ini tidak dapat dinyatakan dengan tepat sebagai bilangan desimal karena tidak ada akhirnya.
1. Ketika 2 l dibagi secara rata kepada 3 anak, berapa l yang akan diterima setiap anak?
A. Warnai bagian untuk 1 anak.
B. Ada berapa l untuk 1 anak?
2/3
Banyaknya bagian untuk 1 anak ketika 1 l dibagi secara rata menjadi 3 bagian adalah 1/3
Banyaknya bagian untuk 1 anak ketika 2 l dibagi secara rata menjadi 3 bagian adalah 2/3.
2 : 3 = 2/3
Carilah jumlah liter susu untuk satu orang saat membaginya di antara ... orang.
- Jika jumlah orang yang akan dibagi dari 1 sampai 5, carilah jumlah liter untuk setiap orang dalam bentuk desimal.
- Jika ada satu dan dua orang, kita bisa mengekspresikannya sebagai bilangan bulat
- Ketika 3 orang, tidak bisa dibagi habis.
- Ketika 4 dan 5 orang, ungkapkanlah dengan desimal
- Apakah mungkin untuk mewakili satu orang dengan jelas ketika ada tiga orang.
- Dengan mengelompokkan bilangan menjadi tiga kategori, dapat diketahui bahwa ada bilangan yang tidak dapat direpresentasikan dengan desimal.
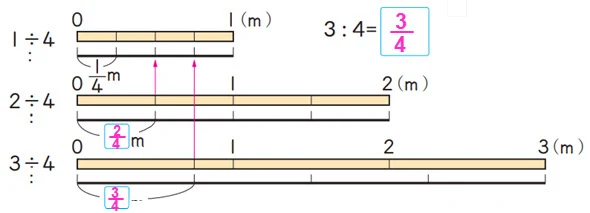
2. Berapa meter panjang setiap bagian jika 3 m tali dibagi menjadi 4 bagian yang sama?
1. Ayo tulislah kalimat matematikanya.
3 : 4
2. Berapakah panjang satu bagian?
3 : 4=3/4
Cara menyatakan panjang 2 m, 3 m, dan 4 m berdasarkan panjang tali yang dibagi menjadi empat bagian yang sama besar 1 m.
- Membagi menjadi 4 bagian yang sama dari 2 m adalah 2/4 m dari tali 1 m. 2 : 4 = 2/4
- 3 meter yang dibagi 4 sama rata adalah 3/4 meter dari tali 1 meter. 3 : 4 = 3/4
Hasil bagi dari masalah pembagian dimana suatu bilangan bulat dibagi dengan bilangan bulat lain dapat dinyatakan sebagai pecahan.
Latihan
Ayo nyatakan hasil bagi menggunakan pecahan.
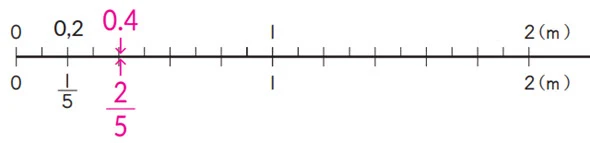
2. Pecahan, Bilangan Desimal, dan Bilangan Bulat 3. Jika kita membagi 2 m pita menjadi 5 bagian yang sama, berapa meter panjang setiap bagian?
1. Ayo nyatakan jawabannya sebagai pecahan dan bilangan desimal.
2: 5 = 2/5 = 0,4
2. Ayo tuliskan posisi pecahan dan bilangan desimal ini dalam garis bilangan.
4. Manakah yang lebih besar 3/5 liter dan 0,7 liter? Jika kita mengonversi pecahan menjadi desimal, kita dapat membandingkannya karena keduanya adalah desimal. Sehingga, 3 : 5 = 0,6, dan 0,7 L yang lebih besar.
Kita juga dapat membandingkan desimal dengan mengubahnya menjadi pecahan dan mencocokkannya dengan pecahan. 0,7 = 7/10. 3/5 = 6/10 , jadi 0,7 L lebih banyak
5. Ayo nyatakan pecahan berikut sebagai bilangan desimal atau bilangan bulat.
6. Ayo nyatakan 2 dan 5 sebagai pecahan.
7. Ayo nyatakan bilangan desimal 0,19 dan 1,7 sebagai pecahan.
1. Karena 0,19 adalah 19 dikalikan dengan 0,01. kita dapat berpikir sebagai 19 dikalikan dengan 1/100 dan mendapat 19/100.
2. Karena 1,7 adalah 17 dikalikan dengan dari 0,1, kita dapat berpikir sebagai 17 dikalikan dengan 17/10 dan1/10 mendapa1 1 7/10.
Bilangan desimal dapat dinyatakan sebagai pecahan jika kita memilih 1/10 dan 1/100 sebagai unitnya.
Latihan
Isilah kotak dengan bilangan desimal dan pecahan.
8. Ayo bagilah pecahan berikut menjadi 3 kelompok.9. Ayo tulislah sebuah tanda panah ↓ untuk setiap bilangan berikut pada garis bilangan di bawah ini.
Bilangan bulat, bilangan desimal, dan pecahan semuanya dapat dinyatakan pada garis bilangan.Hal ini dapat mempermudah untuk membandingkan bilangan tersebut.
Latihan
1. Ayo urutkan bilangan berikut dari yang paling kecil
2. Ayo ubahlah bilangan desimal menjadi pecahan dan pecahan menjadi bilangan desimal atau bilangan bulat
Demikikian pembahasan mengenai Pecahan, Bilangan Desimal, dan Bilangan Bulat. Semoga tulisan ini bermanfaat. Dari pembahasan materi di atas adalah bahwa Cara Menghitung Perkalian dan Pembagian Bilangan Pecahan tidaklah begitu sulit untuk dipahami. Hanya dibutuhkan ketelitian dalam mengalikan angka - angka yang ada pada bilangan pecahan tersebut. Untuk menambah wawasan kalian mengenai materi bilangan pecahan, pelajari juga materi tentang Cara Mengubah Bilangan Pecahan Biasa Menjadi Bilangan Pecahan Campuran. untuk materi bahasa Indonesia Alhamdulillah para murid sudah tuntas memhami kosakata sulit dalam teks bacaan

















Tidak ada komentar:
Posting Komentar